1.)La
prevalencia de la diabetes es del 4%. La glucemia basal diagnóstica
correctamente
el 95% de los
diabéticos, pero da un 2% de falsos positivos. Diagnosticada una persona
¿Cuál es la
probabilidad de que realmente sea diabética?
Solución
Sea D el
suceso de tener diabetes, °D el suceso de no tenerla y Gl+ el suceso de dar
Positivo en
la prueba de la glucemia basal. Los datos del problema nos dicen que:
P(D) = 0,04
P(°D) = 0,96
P(Gl+ / D) = 0,95
P(Gl+ / °D) = 0,02
Entonces el
teorema de Bayes, escrito en los términos de este problema nos dice que:
|
P (Gl+ / D)* P (D) + P
(Gl+ / °D)* P(°D)
|
Sustituyendo por los valores
numéricos
|
0,95*
0,04+ 0,02* 0,96
|
2.) En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.
b. Si el infante
resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.
SOLUCIÓN:
Se definen los sucesos:
Suceso H: seleccionar
una niña.
Suceso V: seleccionar
un niño.
Suceso M: infante
menor de 24 meses.
En los ejercicios de
probabilidad total y teorema de bayes, es importante identificar los sucesos
que forman la población y cuál es la característica que tienen en común dichos
sucesos. Estos serán los sucesos condicionados.
a. En este caso, la
población es de los infantes. Y la característica en común es que sean menores
de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de
24 meses es un ejemplo de probabilidad total. Su probabilidad será:
b. Para identificar
cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir
de reconocer esta es una probabilidad condicionada y que la característica
común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad
de que sea niña una infante menor de 24 meses será:
3.) Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género
masculino
b. Si resulta que es de género masculino, determine la
probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se
refiere a un problema de probabilidad total, ya que es el suceso condicionado y
las cirugías los condicionantes. Dicho valor será:
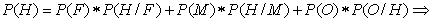

b. Como el suceso
condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el
valor de la probabilidad será:

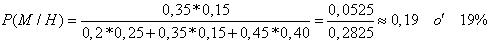
0
comentarios




