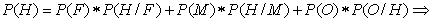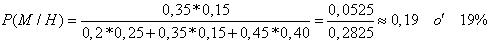Uno
de los objetivos de la estadística es el conocimiento cuantitativo de una
determinada parcela de la realidad. Para ello, es necesario construir un modelo
de esta realidad particular objeto de estudio, partiendo de la premisa de que
lo real es siempre más complejo y multiforme que cualquier modelo que se pueda
construir. De todas formas, la formulación de modelos aceptados por las
instituciones responsables y por los usuarios, permite obviar la existencia del
error o distancia entre la realidad y el modelo. Los modelos teóricos a los que
se hace referencia se reducen en muchos casos a (o incluyen en su formulación)
funciones de probabilidad.
La
distribución de probabilidad es para indicar toda la variedad de valores
médicos que pueden representarse como resultado de un experimento si éste se
llevase a cabo. Es decir, describe la probabilidad de que un evento se realice
en el futuro, constituye una herramienta fundamental para la prospectiva,
puesto que se puede diseñar un escenario de acontecimientos futuros
considerando las tendencias actuales de diversos fenómenos naturales.
Es
importante en la medicina porque me permite conocer la frecuencia de las
enfermedades, y los valores que me arroja luego de aplicar un experimento.
En
el área de la ciencia de la salud las distribuciones de Probabilidad son
importantes ua que estas nos ayudan a representar teóricamente y de forma
simplificada un fenómeno real, conocer la probabilidad de ocurrencia de ciertos
sucesos y se puede conocer el comportamiento de una variable aleatoria. Esto
nos facilita al momento de la toma de
decisiones y la precisión de hechos que puedan ocurrir.
Las
distribuciones de probabilidad en el área de la salud sirven para conocer la
probabilidad de que un evento (enfermedad) ocurra en el futuro, la efectividad
de un medicamento o la falla de el mismo, esto es fundamental debido a que se
pueden tomar las previsiones necesarias ya que se conoce todos los posibles
resultados de dicho evento.
Podeos
encontrar distintas distribuciones de probabilidad
Experimento
de Bernoulli: es un experimento aleatorio en el que sólo se pueden obtener dos
resultados (habitualmente etiquetados como éxito y fracaso).
Un médico realiza una toma de muestra de sangre en un paciente de 13 años
de edad para confirmar un posible caso
de dengue. Considerando el resultado positivo como un fracaso y el resultado
negativo como éxito.
Experimento
Binomial
Se
realiza una prueba de sangre en 10 hombres de 24 – 30 años de edad que han
tenido problemas cardiacos. Considerando el resultado positivo como un éxito y
el resultado negativo como un fracaso.
Ejemplo:
Una
joven estudiante de 20 años de edad necesita saber si se encuentra embarazada,
ya que tiene ausencia de la menstruación, se le realiza un examen de orina,
donde los valores pueden ser positivo o negativo. Dando como resultado
positivo, la joven ya puede estar segura que tendrá un bebe, mientras que la
Doctora tratante obtuvo un diagnostico exitoso. Según la distribución de
Bernoulli que tomo una probabilidad de éxito y una de fracaso
0
comentarios







.jpg)